◀︎ Navigate through the 3D pages ► Next

The Fourier Transform

A sampled function of time on the left, with its spectrum next to it. Both displayed as periodic.

In Brief

Logically, neither signal nor spectrum precedes the other, or are even distinguishable. For introductory purposes the remarks that follow take an applied perspective. A physical measurement takes place in time and is bounded in duration. The resulting spectrum can be used to reconstruct the signal beyond the measured samples, and yields a periodic function of time — with possible “glitches” at the boundaries, which have become implicitly linked. The next section presents some fundamental examples.

See Also


Try It Yourself


Rotate the signal

Magnify the signal

Draw the signal

Expand the time axis




Functions of time ✼

  • 1-second sampling function
  • 1 second (1 Hz) waves
  • DC = (= 𝐹𝑁) = full-scale
  • δ(t) + i ∙ ℋ{ δ(t) }
  • Your turn    Try these
    • Real:  
    • Imag:  
Rotate the spectrum

Magnify the spectrum

Draw the spectrum

Expand the frequency axis




Functions of frequency ✼

  • 1 Hz sampling function
  • Your turn    Try
    • Real:  
    • Imag:  

Remarks

A general discussion of samples and sequences would include these talking points:

By contrast, this section takes a stereotypical (verging on dogmatic) laboratory perspective:

We choose the number of data points N as 256 for adequate screen resolution. N is dimensionless: the DFT does not come equipped with units. Its functions are defined on the bare integers only.

A real-world measurement will most surely have units. A Hertz is no “smaller” or “larger” than a second, but the coincidence of the sha function Ш in both domains is important. They are the first two examples above. The criterion that

implies that

which in turn yields the calibration described below.

Caveat Lector

It is easy to assume that ΔF = 1 / ΔT 🚫 and ΣF = 1 / ΣT 🚫 but neither is true.

Time

  1. ΣT ≡ √N = 16 s = measurement duration = sample range
This duration must be the sum of time between samples (hence the notation):
ΣT = 𝚺1..NΔT = N∙ΔT
so ΔT is now determined as:
  1. ΔT = ΣT / N = 1/16 s = sampling interval 𝑇s = time resolution

Display

It is physically intuitive to treat time as one-sided, running from zero (start of measurement) to ΣT (end of measurement) in steps of ΔT.

Human-readable displays usually show time as one-sided. There is no requirement that the last half of the samples be zero. The display above starts the signal at time zero, and draws more than two full measurement durations.

  • The one-sided time range 0..16 s is shaded blue (real) or red (imaginary) on some example signals.

However...you will find when entering custom functions that it does indeed matter which range you use. Try this experiment.

  1. Tap the button to generate an expression for a familiar function of time
  2. Tap the button to generate the signal and spectrum
  3. Tap the button to generate the signal and spectrum
  4. Tap the button to get another function
  5. Repeat steps 2 and 3

At this point the we switch over to the other column for steps 3 and 4. The half-values are so directly dependent on the full values that they come as afterthoughts.

The half-value

This is primarily just for symmetry in the equations.

  1. QT = ΣT / 2 = 8 s

One is tempted to call this the “Nyquist” time 𝑇𝑁, but it depends on how you want the analogy to work. If you want it to mean the time beyond which the signal must be zero,” then 𝑇𝑁 should be the measurement duration ΣT = 16 s.

Two-sided time

When drawing a sampled (hence implicitly periodic) time domain as literally circular, it is natural to treat the “last” samples as being in negative time, although events in the “negative half” did not really precede events in the positive half.

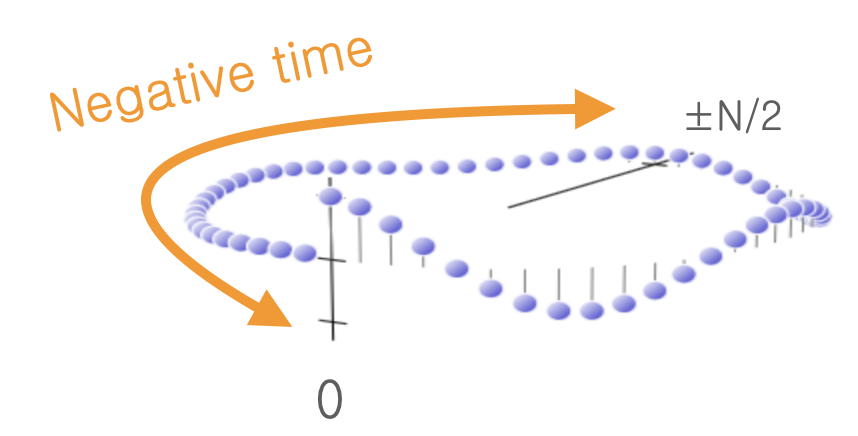
Bracewell Ring
  • Some smoothing functions are extended (in lighter gray) to the two-sided time range -8..8 s.

Frequency

The reciprocal of 𝑇s from step 2 must be 𝐹s:

  1. ΣF = 1 / ΔT = 16 Hz = sample rate 𝐹s= measurement bandwidth
As the bandwidth, ΣF must also be the sum of ΔF:
ΣF = 𝚺1..NΔF = N∙ΔF
so ΔF is derived as:
  1. ΔF = ΣF / N = 1/16 Hz = frequency resolution

Display

It is less plausible to treat frequency as one-sided, running from zero (DC) to ΣF.

Human-readable spectra usually omit the redundant bins, or display them as two-sided. When the signals are real, the spectra have even magnitude. The display above centers the frequency at zero, and draws more than two full measurement durations.

  • The two-sided frequency range -8..8 Hz is shaded blue (real) or red (imaginary) on some example signals.

The half-value

This is important enough for its own name and symbol

  1. QF = ΣF / 2 = 8 Hz = 𝐹𝑁 = Nyquist frequency

It is a prerequisite for unambiguous sampling that a signal have no components above 𝐹𝑁. The spectrum values that a DFT provides in the “high half” do not represent beyond-Nyquist frequencies, but negative frequencies paired with positive ones. The information in N real samples is the same as in N/2 complex spectral values.

This apparent asymmetry between the domains’ internal symmetry can be avoided by using the Cosine or Hartley transform.

Two-sided frequency

Drawing a sampled (implicitly periodic) frequency domain as literally circular poses fewer conceptual blocks, because the idea of negative frequency does not seem to raise issues of causality.

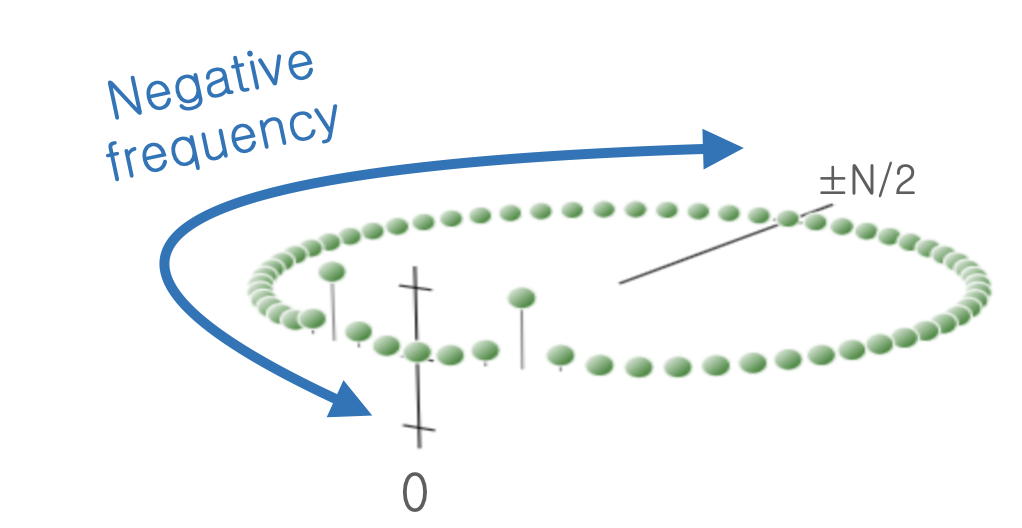
Bracewell Ring
  • Smoothing functions are shown over the two-sided frequency range -8..8 Hz.

✼ More discussion coming


◀︎ Navigate through the 3D pages ► Next